Substitute the values of a a, d d, and e e into the vertex form a ( x d) 2 e a ( x d) 2 e 2 x 2 2 x 2 2 x 2 2 x 2 Set y y equal to the new right side y = 2 x 2 y = 2 x 2 y = 2 x 2 y = 2 x 2 Use the vertex form, y = a ( x − h) 2 k y = a ( x h) 2 k, to determine the values of a a, h h, and k kSebagai contoh pada persamaan y = 2x 21 Parabola ini akan berbentuk seperti huruf "U" karena variabel a bernilai positif, yaitu 2 Jika ada variabel y kuadrat dan bukan x kuadrat dalam persamaan Anda, parabola akan membuka ke samping, ke kananA y 2&'x 32 6c y 2&'x 32 6 b y &'x 32 6 d y 2&'x 32 6 Factor the expression ____ 2 x2 11x 28 a (x 7)(x 4)c (x 4)(x 7) b (x 7)(x 4)d (x 4)(x 7) ____ 3 6x2 4x 8 a 6x(3x 2) c 6x2 4x 8 b 3(2x2 4x 8)d 2(3x 2x 4) ____ 4 12x2 8x a x( 12x 8)c 12x(x 2) b 4x(3x 2)d 3x(x 4 2) Identify the vertex and the axis of symmetry of the parabola

Graphing Parabolas
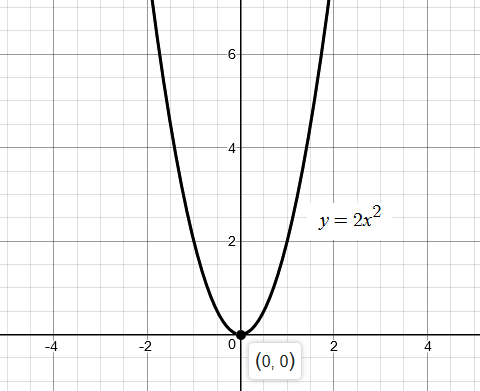
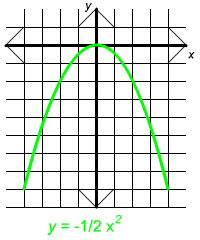
Parabola of y 2x 2
Parabola of y 2x 2-The Vertex of a Parabola There are two methods to obtain the coordinates of the vertex of a parabola In the first method, we can use the direct result x= −( b 2a) x = − ( b 2 a) whileY=2x^2 What is the vertex?




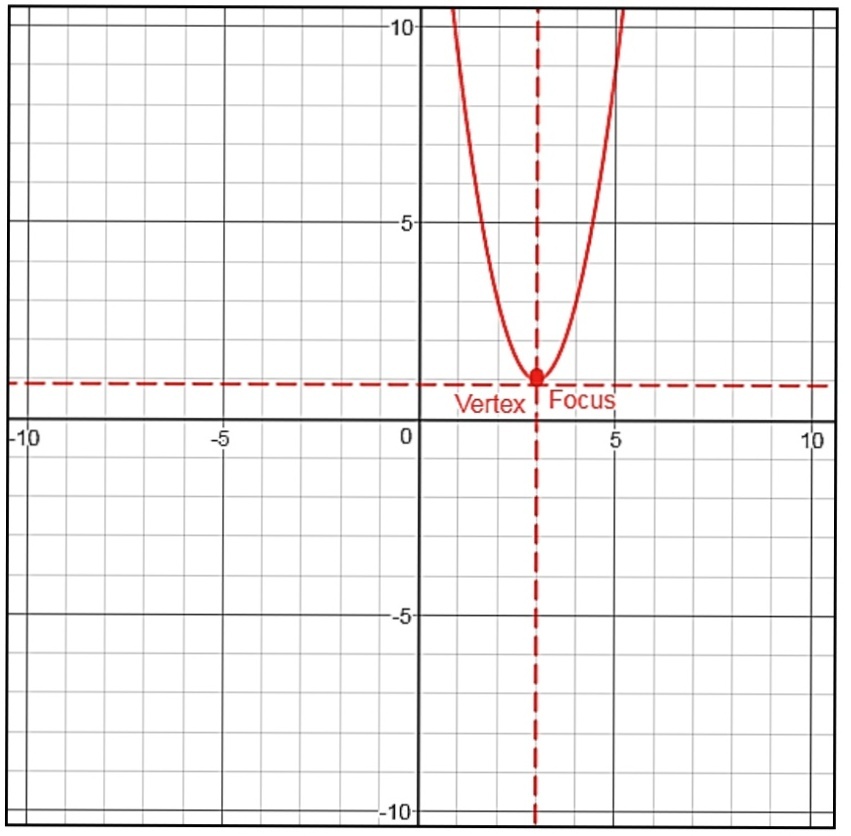
Focus Of Parabola Y 2x 2 X
Answer y = x^2 3x = x \\cdot (x3) is an upwardopening parabola y = 2x is a straight line which intersects the parabola when x^2 3x = 2x \\rightarrow x^2 5x = 0 \\rightarrow x \\cdot (x 5) = 0 \\rightarrow x = 0 or x = 5 \\rightarrow (0, 0) and (5, 10) y = x is a straight line which iFor the parabola y' = x/2y At the point (1,1) the product of the slope of the tangents is 1 The same is the case at (1, 1) This shows that the ellipse 2x^2y^2= 3 and the parabola y^2= x areExploring Parabolas y = ax^2 bx c Exploring Parabolas by Kristina Dunbar, UGA Explorations of the graph y = a x 2 b x c In this exercise, we will be exploring parabolic graphs of the form y = a x 2 b x c, where a, b, and c are rational numbers In particular, we will examine what happens to the graph as we fix 2 of the values for a, b, or c, and vary the third
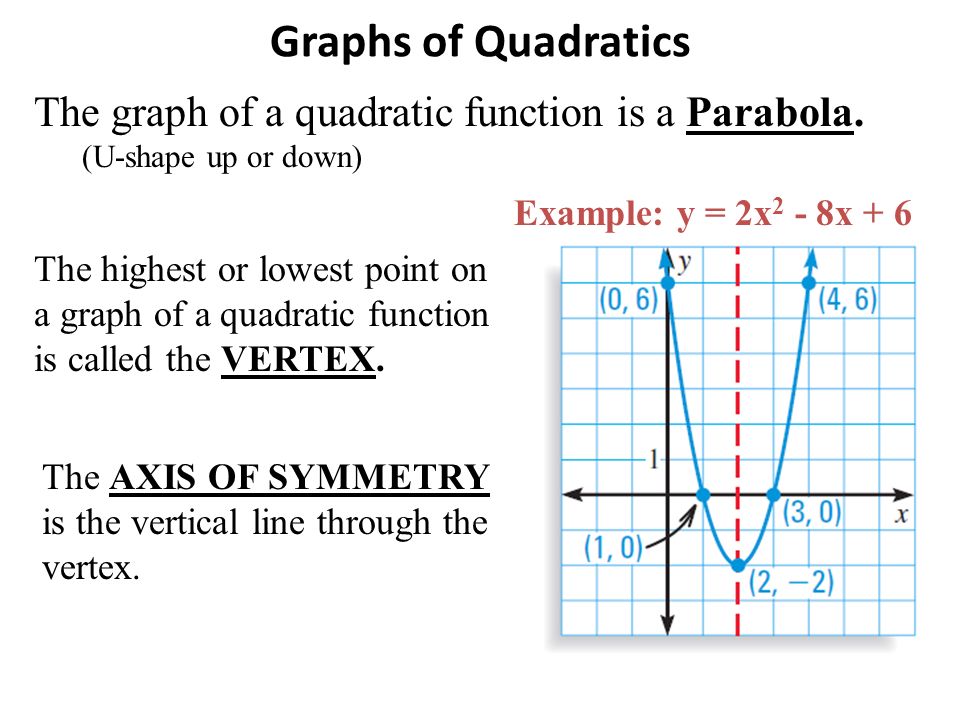
A Quadratic Equation takes the form y = ax2 bx c Graph of a quadratic function forms a Parabola The coefficient of the x2 term (a) makes the parabola wider or narrow If the coefficient of the x2, term (a) is negative then the parabola opens down The term Vertex is used to identify the Turning Point of a parabolaStandard equation of a parabola that opens up and symmetric about xaxis with at vertex (h, k) (y k)2 = 4a (x h) Graph of y2 = 4ax Axis of symmetry x axis Equation of axis y = 0 Vertex V (0, 0) Focus F (a, 0) Equation of latus rectum x = a Equation of directrix x = aThe standard equation of a parabola is y = a x 2 b x c But the equation for a parabola can also be written in "vertex form" y = a ( x − h ) 2 k In this equation, the
What is the following parabola's axis of symmetry of y = x 2 − 2 x − 3 Since this equation is in standard form, use the formula for standard form equation x = − b 2 a Answer the axis of symmetry is the line x = 1 Problem 7Given \(y = x^2 2x 3\) If the parabola is shifted \(\text{1}\) unit to the right, determine the new equation of the parabola If the parabola is shifted \(\text{3}\) units down, determine the new equation of the parabolaThe Parabola Given a quadratic function f ( x) = a x 2 b x c, it is described by its curve y = a x 2 b x c This type of curve is known as a parabola A typical parabola is shown here Parabola, with equation y = x 2 − 4 x 5



Organize The Information For Your Parabola Graph Your Parabola Y 2x 2 12x 19 Axis Of Symmetry Snapsolve




Parabola Sketching Y 2x 2 4x 6 From The Parabola Translation Download Scientific Diagram
Let us understand with the help of examples Graphing Parabola Solved Examples Example 1 Draw a graph for the equation y = 2x 2 x 1 Solution The given equation is y = 2x 2 x 1 Here, a = 2, b = 1 and c = 1X = y 2 2 x = y 2 2 x = y 2 2 x = y 2 2 Use the vertex form, x = a ( y − k) 2 h x = a ( y k) 2 h, to determine the values of a a, h h, and k k a = 1 2 a = 1 2 h = 0 h = 0 k = 0 k = 0 Since the value of a a is positive, the parabola opens right Opens Right Find the vertex ( h, k) ( h, k) Let's take a look at the first form of the parabola f (x) = a(x −h)2 k f ( x) = a ( x − h) 2 k There are two pieces of information about the parabola that we can instantly get from this function First, if a a is positive then the parabola will open up and if a a is negative then the parabola will open down



Quadratics Graphing Parabolas Sparknotes



How Do You Use The Important Points To Sketch The Graph Of Y 2x 2 Socratic
This video shows how to take the graph of y = x^2 and stretch it vertically by a factor of 2 Finding the yintercept of a parabola can be tricky Although the yintercept is hidden, it does exist Use the equation of the function to find the y intercept y = 12 x2 48 x 49 The yintercept has two parts the xvalue and the yvalue Note that the xvalue is always zero So, plug in zero for x and solve for yAlso graph the parabola If you can please include the points that I have to graph/plot that would be great I know how to get the vertex but I always mess up when it comes to graphing the exact point or points Answer by ewatrrr(243) (Show Source)



Draw The Graph Of Y 2x 2 3x 5 And Hence Solve 2x 2 4x 6 0 Y 2x 2 3x 5 Sarthaks Econnect Largest Online Education Community




Content Transformations Of The Parabola
The ycoordinate for the line is calculated this way y = 15x 5 The ycoordinate for the parabola is calculated this way y = 2x 2 12x 13 Setting the two ycoordinates equal looks like this 15x 5 = 2x 2 12x 13 When we solve the above equation, we find the xcoordinates for the points of intersection Here's the algebra Best answer Given Two curves are y2 = 4x and y = 2x – 4 Now to find the area between these two curves, we have to find common area ie Shaded portion Intersection of parabola y2 = 4x with line y = 2x – 4 Putting the value of y from the equation of a line in parabola equation, we get, y2 = 4x ⇒ (2x – 4)2 = 4xStep 2) Find two points to the left of the axis of symmetry Let's find the y value when Start with the given equation Plug in Square to get Multiply and to get Combine like terms So the first point to the left of the axis of symmetry is (2,9) Let's find the y value when Start with the given equation Plug in Square to get



Given Y 2x2 Domain Rangs Opening Of The Parabola Gauthmath
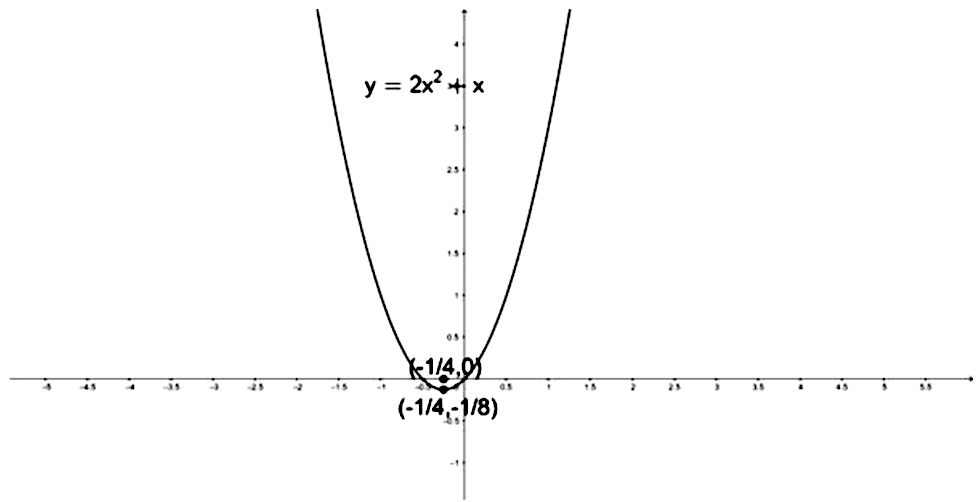



The Focus Of The Parabola Y 2x 2 X Is A 0 0 B 1 2 1 4 C 1 4 0 D 1 4 1 8 Snapsolve
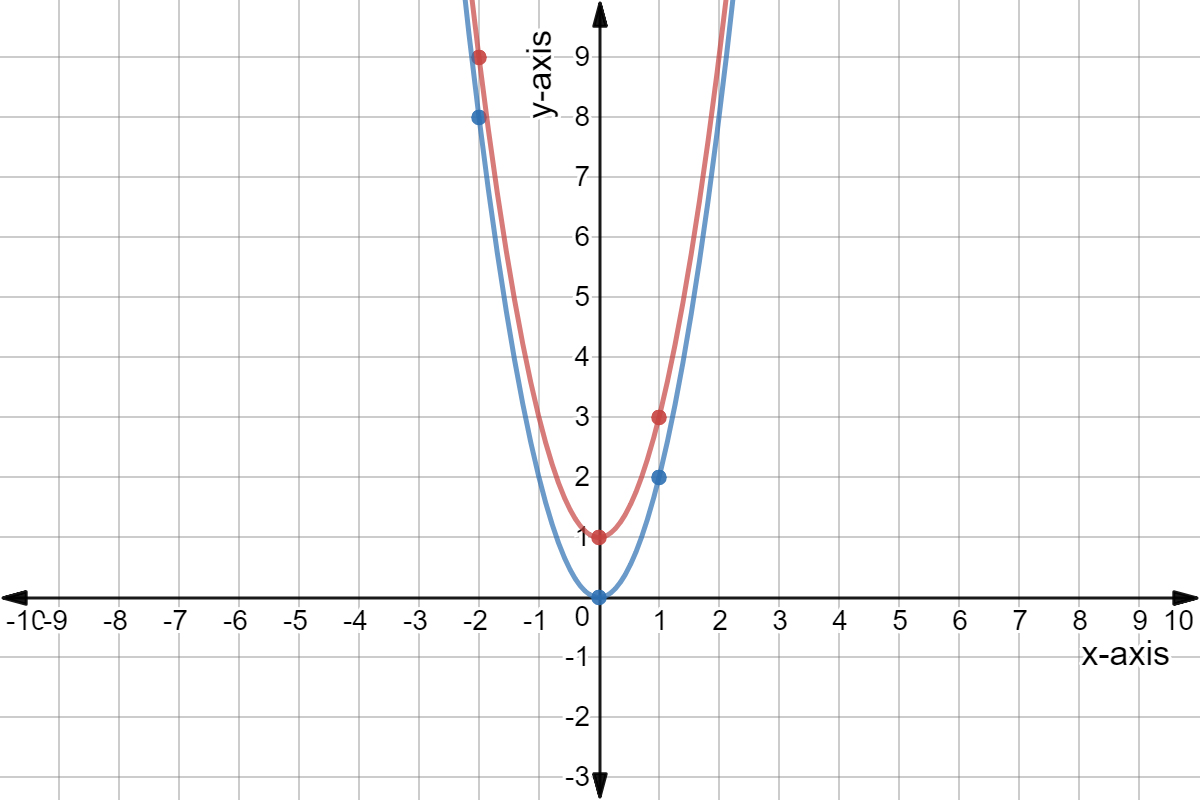
In comparing the graphs of y = x 2 (red), y = 2x 2 (green), and y = 4x 2 (blue), we see that each parabola opens upward but the larger the value of "a", the steeper (narrower) the graph Thus, when a ³ 1, the parabola opens upward, and as the value of "a" increases, the shape of the parabola narrowsThe area of the region bounded by parabola y^2 = x and the straight line 2y = x is asked in Calculus by Chandan01 (512k points) application of integral; A parabola has its vertex and focus in the first quadrant and axis along the line If the distances of the vertex and focus from the origin are respectively , then equation of the parabola is Let y=x1 is axis of parabola, yx4=0 is tangent of same parabola at its vertex and y=2x3 is one of its tangents




Graph The Quadratic Functions Y 2x 2 And Y 2x 2 4 On A Separate Piece Of Paper Using Those Graphs Compare And Contrast The Shape And Position Of The Graphs Study Com



What S The Axis Of Symetry Vertex And Graph Y 2x 2 6x 1 Mathskey Com
Y = m x b and that its graph is a line In this section, we will see that any quadratic equation of the form y=ax2bxc y = a x 2 b x c has a curved graph called a parabola The graph of any quadratic equation y = a x 2 b x c y = a x 2 b x c, whereParabola y =2 x to the parabola y = 2 x 2 The solid lies between planes perpendicular to the xaxis at x =1 and x = 1 The crosssections perpendicular to the xaxis are circular disks whose diameters run from the parabola y = x2 to the parabola y = 2 x2 y !Find the points of intersection of the parabola with the line given respectively by their equations y = 2 x 2 4 x 3 2y x = 4 Solution to Example 1 We first solve the linear equation for y as follows y = (1 / 2) x 2 We now substitute y in the equation of the parabola by (1 / 2) x 2 as follows (1 / 2) x 2 = 2 x 2 4 x 3



Solve And Graph Quadratic Function 2x 2 12x 11 Mathskey Com




Graph The Parabola Y 2x 2 4x 1 Youtube
Write the equation of the parabola in standard form and find its vertex y= 2x^2 4x 8 = 0 When a parabola represented by the equation y 2x 2 = 8 x 5 is translated 3 units to the left and 2 units up, the new parabola has its vertex atSolutions to the Above Questions and Problems Solution The x intercepts are the intersection of the parabola with the x axis which are points on the x axis and therefore their y coordinates are equal to 0 Hence we need to solve the equation 0 = x 2 2 x 3 Factor right side of the equation (x 3) (x 1) () = 0
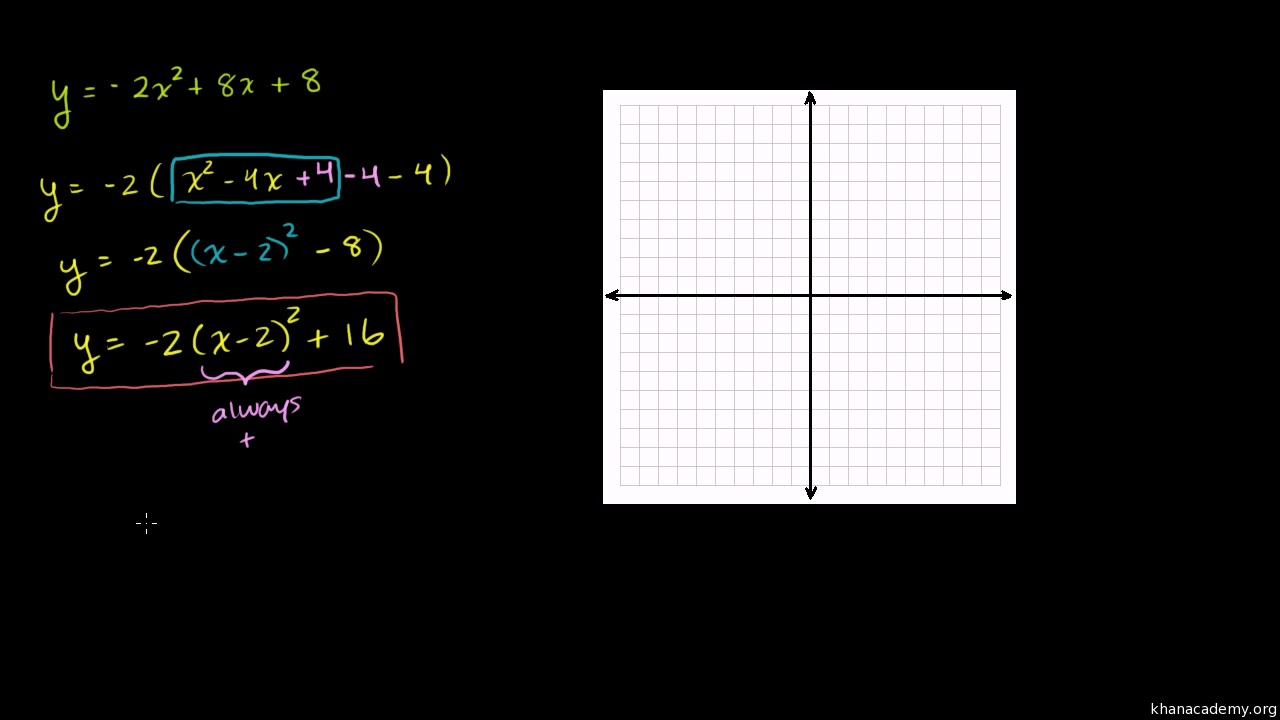



Vertex Axis Of Symmetry Of A Parabola Video Khan Academy



Y2x2 5 ニスヌーピー 壁紙
Calculadora gratuita para parábolas Calcular los focos de una parábola, sus vértices, ejes y su directriz paso por pasoPARABOLAS TRANSLATIONS AND APPLICATIONS QUADRATIC RELATION A quadratic relation in two variables is a relation that can be written in the form y=ax^2bxc or x=ay^2byc where a, b, and c are real numbers, and a!=0 The graphs of quadratic relations are called parabolas The simplest quadratic relation of the form y=ax^2bxc is y=x^2, with a=1, b=0, and c=0, so thisAnswer Correct option is B y = 0 The axis of symmetry of a parabola is a vertical line that divides the parabola into two congruent halves y2 2x = 0 y2 = −2x is the equation of a parabola It is in the form of y2 = 4ax So axis of parabola will be xaxis ( y = 0) as shown in the given figure Answer verified by Toppr



Instructional Unit The Parabola Day 4 And 5



Solution Graph The Parabola Y 2x 2 4x 6 On Graph Paper
The equation of the vertical line is $x = 3$ Area of the region bounded by the parabola $y = 2x^2$, the tangent line to this parabola at $(3; Equations with the yvariable squared will graph as parabolas that open LEFT To put all of this information together, let's look at a few examples of quadratic equations 1 y=2×23x6 This is a standard form quadratic equation with the xvariable squared and a=2 Because a>0, the parabola will open "up" 2 y=4(x3)22Next, let's take the derivative of the parabolic equation, and set the derivative equal to 2 (because the slope of the tangent is 2) y' = 2x a = 2 Substitute for x once more, and solve for a 2(4) a = 2 — > a = 2 8 = 6 Solve for b in the first equation in the system through substitution 4(6) b = 17 — > b = 17 24 = 7



Exploration Of Parabolas




Please Help Thank You The Graph Of The Function Y X2 Is Shown How Will The Graph Change If Brainly Com
Y = x 22x3 at which the tangent is parallel to the x axis Solution y = x 22x3 If the tangent line is parallel to xaxis, then slope of the line at that point is 0 Slope of the tangent line dy/dx = 2x2 2x2 = 0 2x = 2 x = 1 By applying the value x = 1 in y = x 22x3, we get y = 123 y = 4Examples (y2)=3(x5)^2 foci\3x^22x5y6=0 vertices\x=y^2 axis\(y3)^2=8(x5) directrix\(x3)^2=(y1) parabolaequationcalculator y=2x^{2}Equation of normal y = mx−12m−6m3 is parallel to y = 2x3 y = 2x3 is of the form y = mxc where slope m= 2 Substituting m = 2 in the above equation we get y = mx−12m−6m3 = 2x−12×2−6×23 = 2x−72 is the required equation of the normal Distance between y =2x3 and y = 2x−72 is d = ∣∣∣∣∣




Solved Find The Area Of The Region Enclosed By The Parabolas Chegg Com



How Do You Graph Y 2x 2 4x 3 Mathskey Com
2 " x2 2 0 x y 3Y 2 = 8x y 2 = 4px 4p = 8 p = 2 Titik focus adalah (p,0), sehingga titik fokusnya (2,0) Garis direktris adalah garis x = p, sehingga persamaan garis direktrisnya x = 2 Panjang Latus rectum adalah 4p, sehingga Panjang latus rectumnya adalah 8 02 Tentukan titik fokus, garis direktis, dan latus rectum dari parabola 2x 2 32y=0 Jawab0 votes 1 answer Find the area of the common region bounded by x^2 y^2 = 16 and parabola y^2 = 6x




Characteristics Of Parabolas College Algebra



Parabolas And Cubics
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Y= (xh)^2 k with (h,k) being the vertex, this parabola has a vertex at (0, 1/4) If you are trying to factor it to find the xintercepts (aka the roots, the zeroes, or the solutions), this is also really easy, as the equation is a difference of perfect squares and can be factored into conjugates, l y = −√x (the bottom half of the parabola) Here is the curve y 2 = x It passes through (0, 0) and also (4,2) and (4,−2) Notice that we get 2 values of y for each value of x larger than 0 This is not a function, it is called a relation Example 7 (y 1) 2 = x



Quadratic Graph Example Y Ax C Expii



The Area Common To The Parabola Y 2x 2 And Y X 2 4 Is A 2 3 Sq Units Sarthaks Econnect Largest Online Education Community
Calculate parabola directrix given equation stepbystep \square!18)$, and the $x$axis $=$(area of the region bounded by the parabola $y = 2x^2$and



Quadratics Graphing Parabolas Sparknotes



Solution Graph Y 2x 2 4x



What Is The Maxima And Minima Global And Local Of The Function Y 2x X 2 Explain It With The Help Of A Graph Quora



1



1




Find The Point On The Parabola Y 2 2x Which Is Closest To The Point 1 4



Parabola Y X 2 Geogebra




Parabolas Xcelerate Math
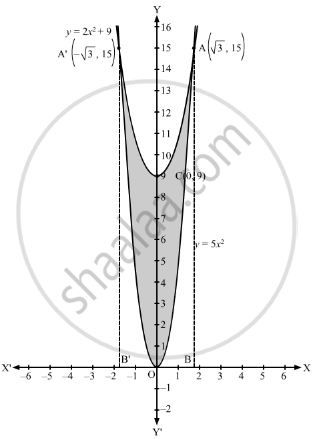



Find The Area Enclosed By The Parabolas Y 5x2 And Y 2x2 9 Mathematics Shaalaa Com
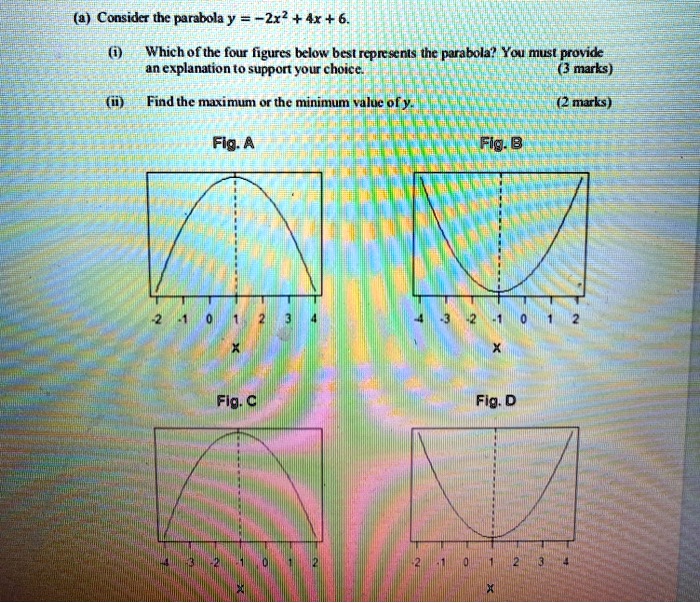



4 Considcr The Parabola Y 2x2 4x 6 Which Of T Itprospt



Solution How To Graph Y 2x 2 1
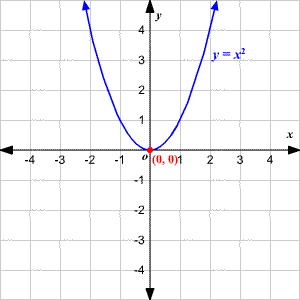



Parabolas



What Is The Vertex Of Y 2x 2 4x 12 Socratic



How To Find The Equation Of The Axis Of Symmetry For Y 2x 2 4x 6 Quora
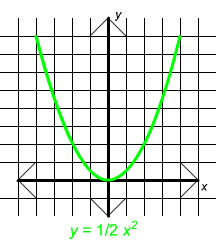



Parabolas And Cubics



How Do You Find The Vertex Of The Parabola Y 2x 2 8x 7 Socratic



Exploration Of Parabolas



How Do You Find The Vertex Of Y 2x 2 4x Socratic




Focus Of Parabola Y 2x 2 X




Graph The Parabola And Give Its Vertex Axis X Intercepts And Y Intercept Y 2x 2 8x 16 Study Com




How To Graph A Parabola 13 Steps With Pictures Wikihow
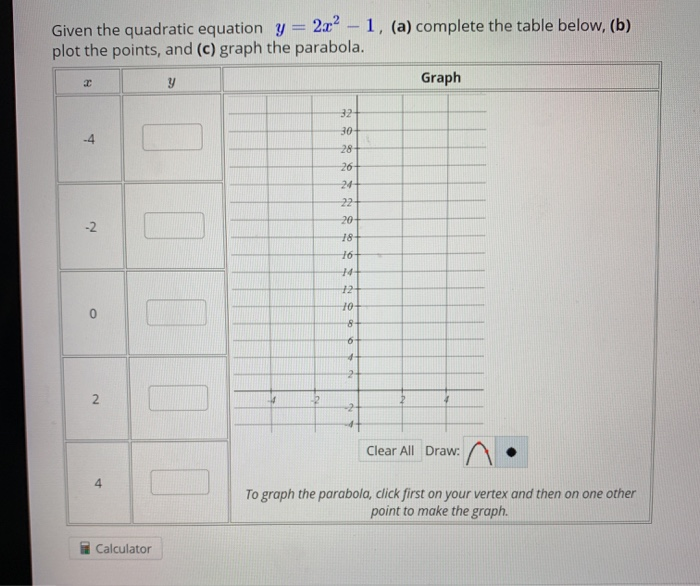



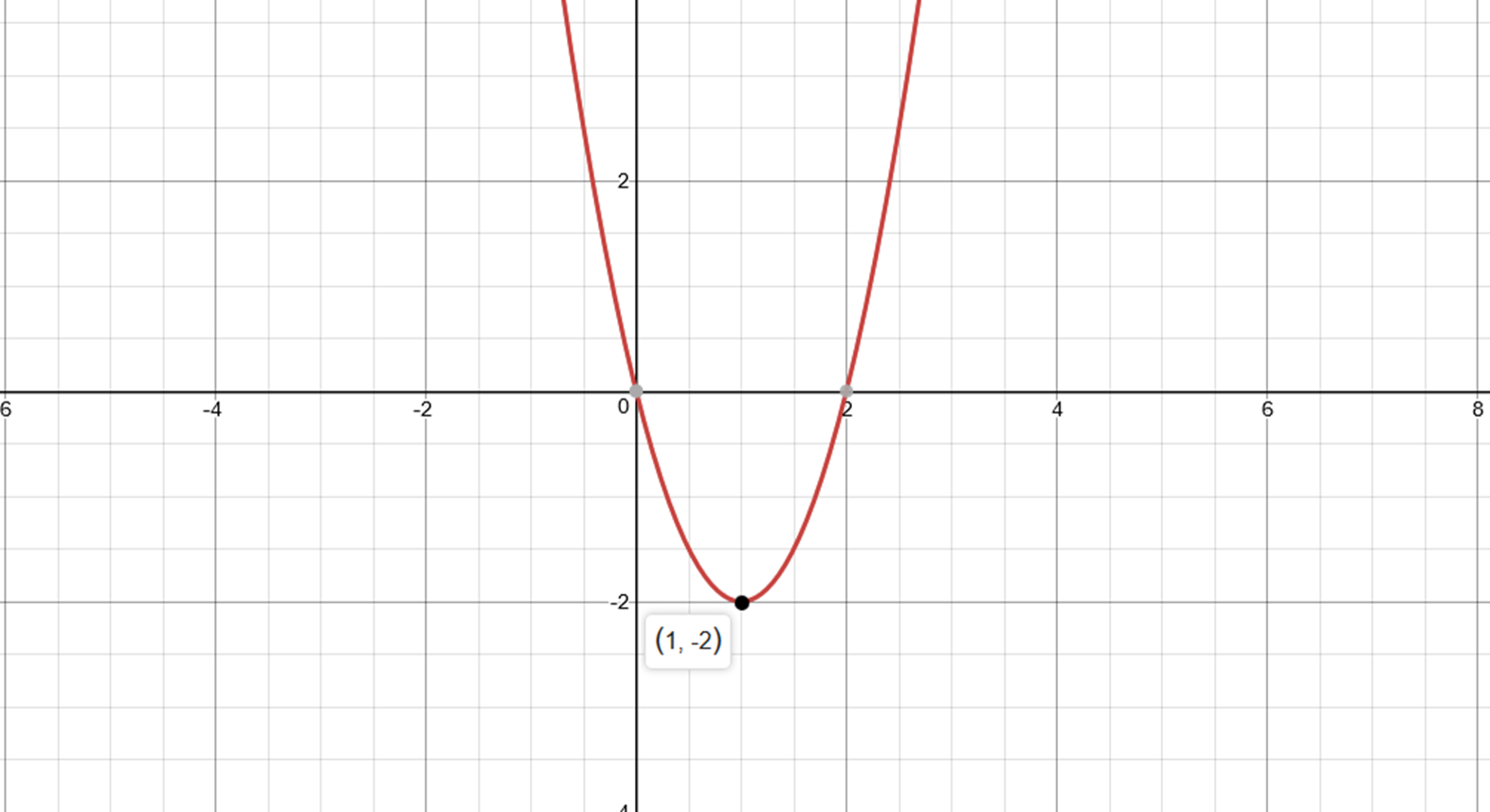
Solved Given The Quadratic Equation Y 2x2 1 A Complete Chegg Com




Mfg Graphing Parabolas



Exploration Of Parabolas
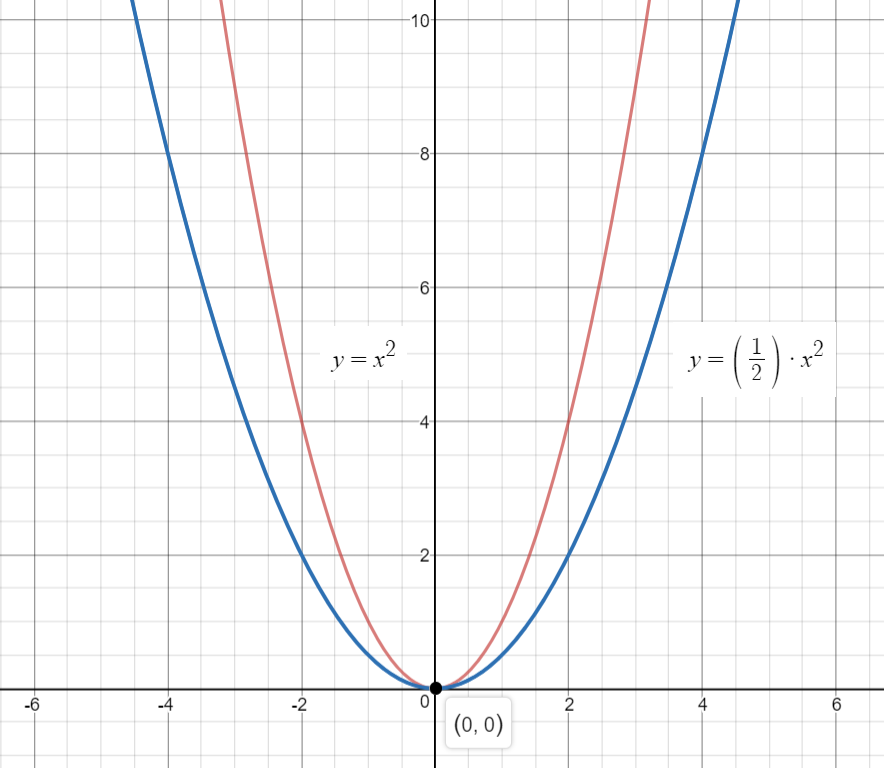



How Do You Sketch The Graph Of Y 1 2x 2 And Describe The Transformation Socratic




Ex 8 2 7 Mcq Area Lying Between Y2 4x And Y 2x Is



Graph The Parabola Y X 2 6x Mathskey Com




Graph The Quadratic Functions Y 2x 2 And Y 2x 2 4 On A Separate Piece Of Paper Using Those Graphs Compare And Contrast The Shape And Position Of The Graphs Study Com
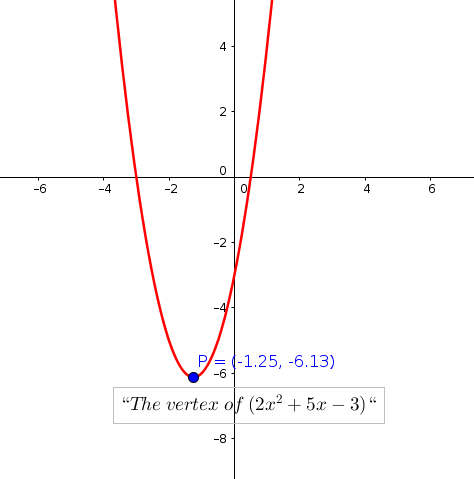



What Is The Vertex Form Of Y 2x 2 5x 3 Socratic




Find The Vertex Of The Parabola Whose Equation Is Y 2x2 8x 5




Graphing Parabolas



For What Values Of B Will The Straight Line Y 2x B Not Intersect The Parabola Y X 2 3x 5 Math Homework Answers




Graphing Parabolas
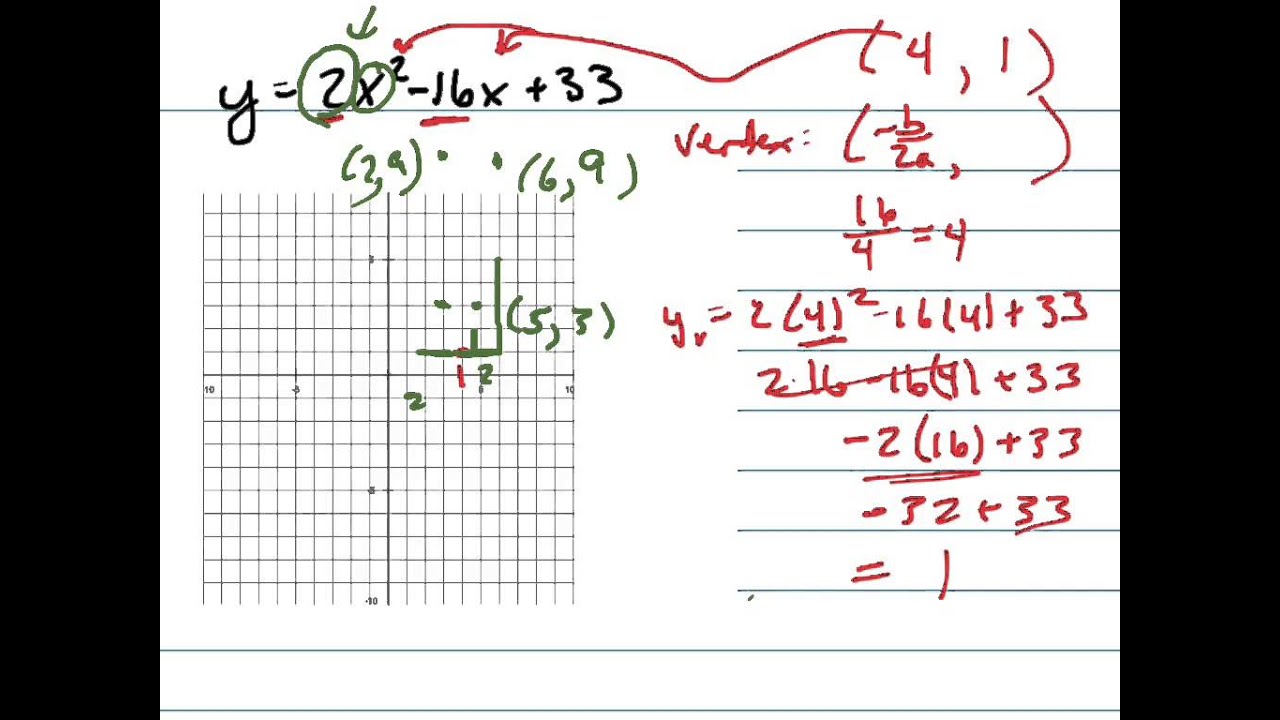



Graph Y 2x 2 16x 33 Youtube



Solution I Have To Find The Vertex Axis Of Symmetry Minimum Or Maximum Value And Range Of The Parabola The Formula Is Y Ax 2 Bx C Question Y 2x 2 6x 3 What I Have So Far Y 2x 2 6x
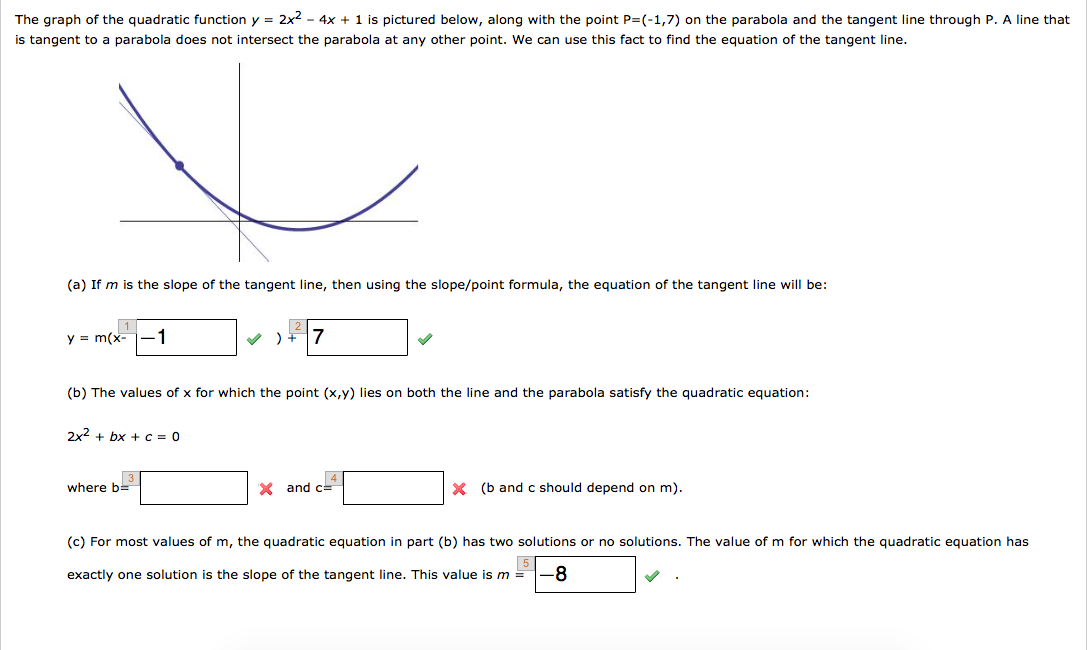



Solved The Graph Of The Quadratic Function Y 2x 2 4x 1 Chegg Com



Warm Up Graphing Using A Table X Y 3x 2 Y 2 Y 3 2 2 8 Y 3 1 Y 3 0 Y 3 1 Y 3 2 2 4 Graph Y 3x Ppt Download




Solved Find The Area Of The Region Enclosed By The Chegg Com



Solution Identify The Coordinates Fo The Vertex And Focus The Equations Of The Axis Of Symmetry And Directrix And The Direction Of Opening Of The Parabola With Equation Y 2x 2 16x 27



Solution Find The Vertex Of The Parabola Y 2x2 12x 13
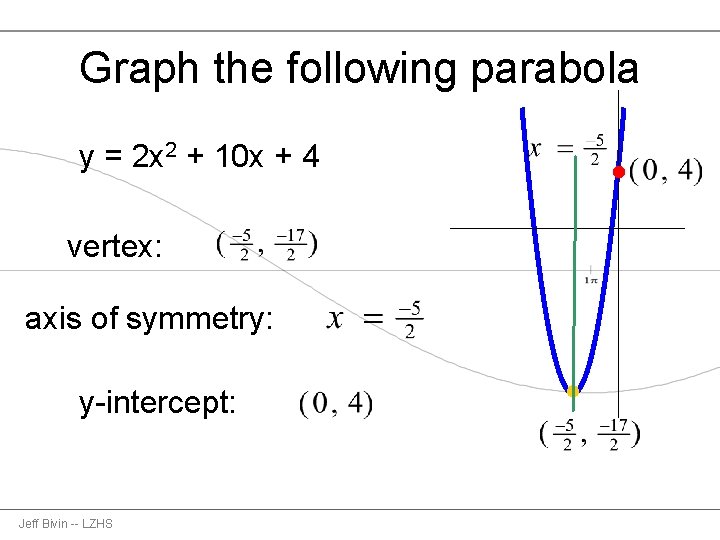



Graphing Parabolas Using The Vertex Axis Of Symmetry
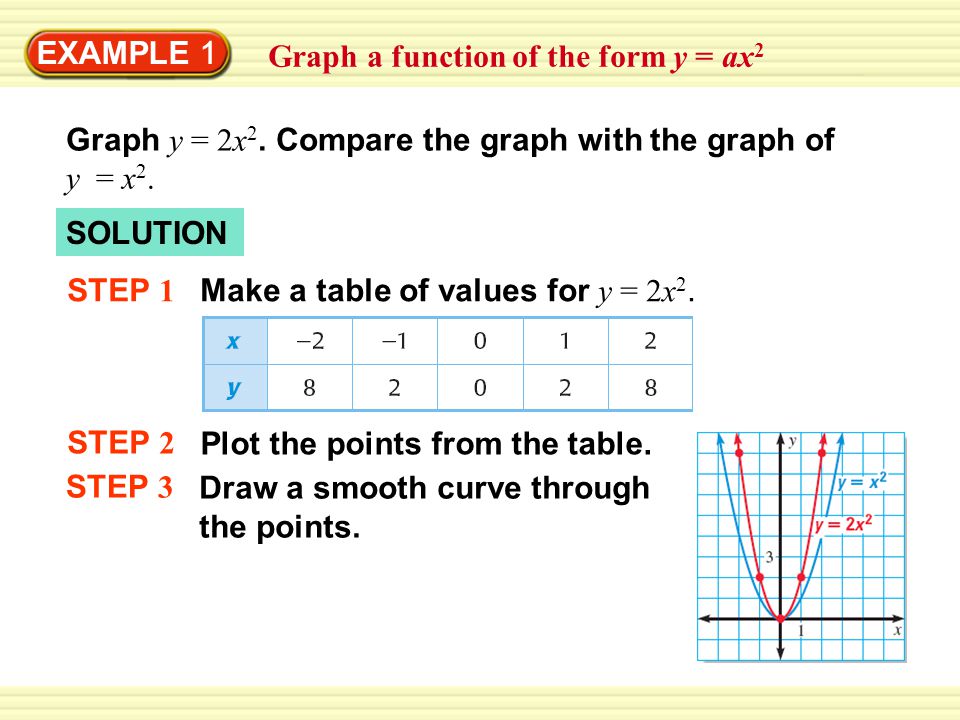



Example 1 Graph A Function Of The Form Y Ax 2 Graph Y 2x 2 Compare The Graph With The Graph Of Y X 2 Solution Step 1 Make A Table Of Values For Ppt Download




Find The Vertex Of The Parabola Y 2x2 10x 8 Brainly Com




Solved The Graph Of The Quadratic Function Y 2x2 4x 1 Is Pictured Below Along With The Point P 1 7 On The Parabola And The Tangent Line Through P A Line That




Points A And B Lie On The Parabola Y 2x 2 4x 2 Such That The Origin Is The Mid Point Of The Line Segment Ab Mathematics Stack Exchange
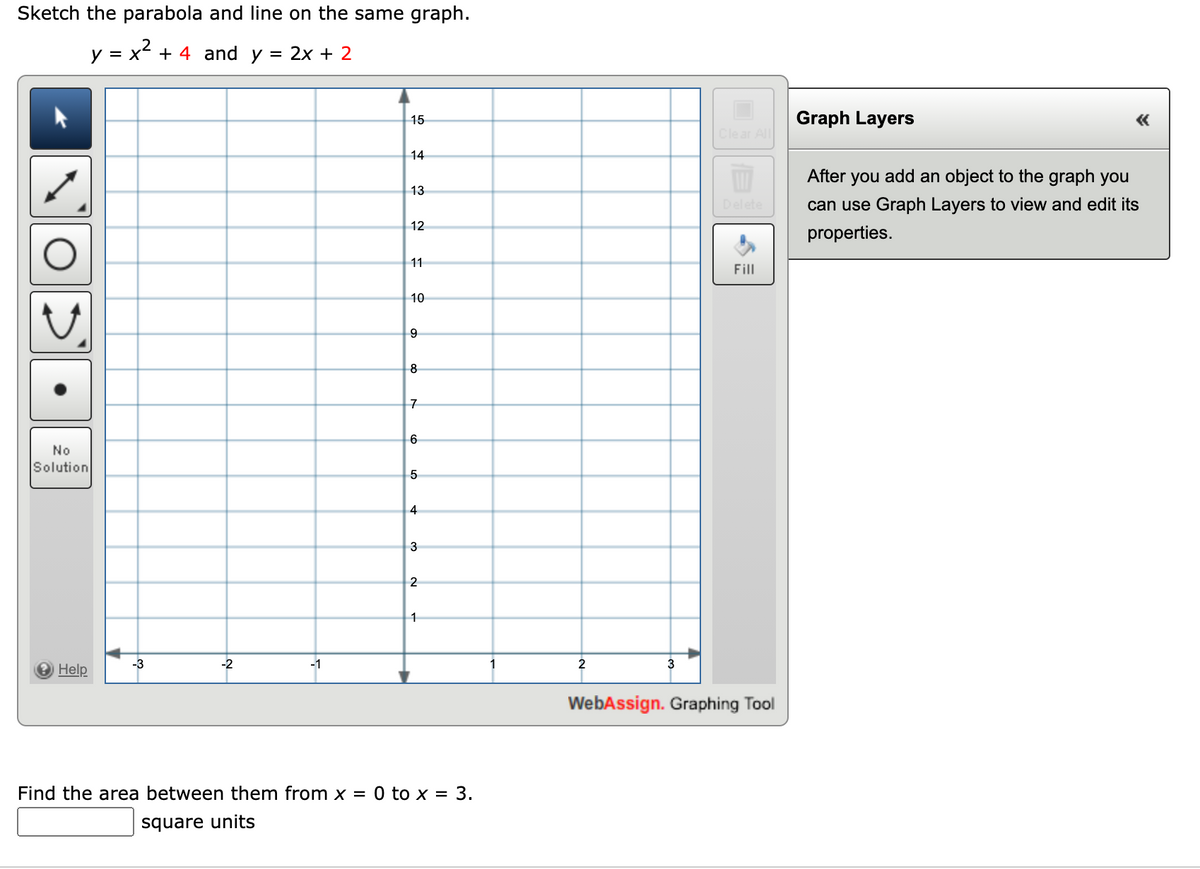



Answered Sketch The Parabola And Line On The Bartleby



Graphs Of Functions Y X2 Y 2x2 And Y 2x2 In Purple Red And Blue Respectively
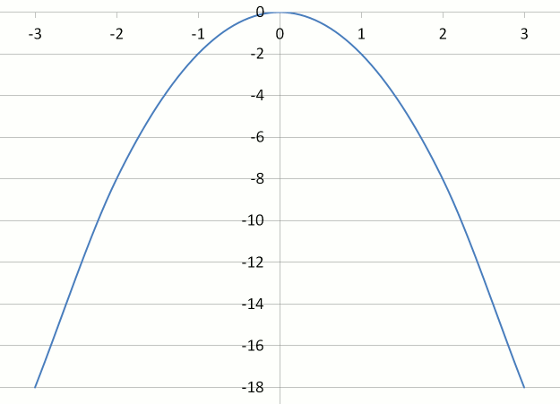



Parabolas Xcelerate Math
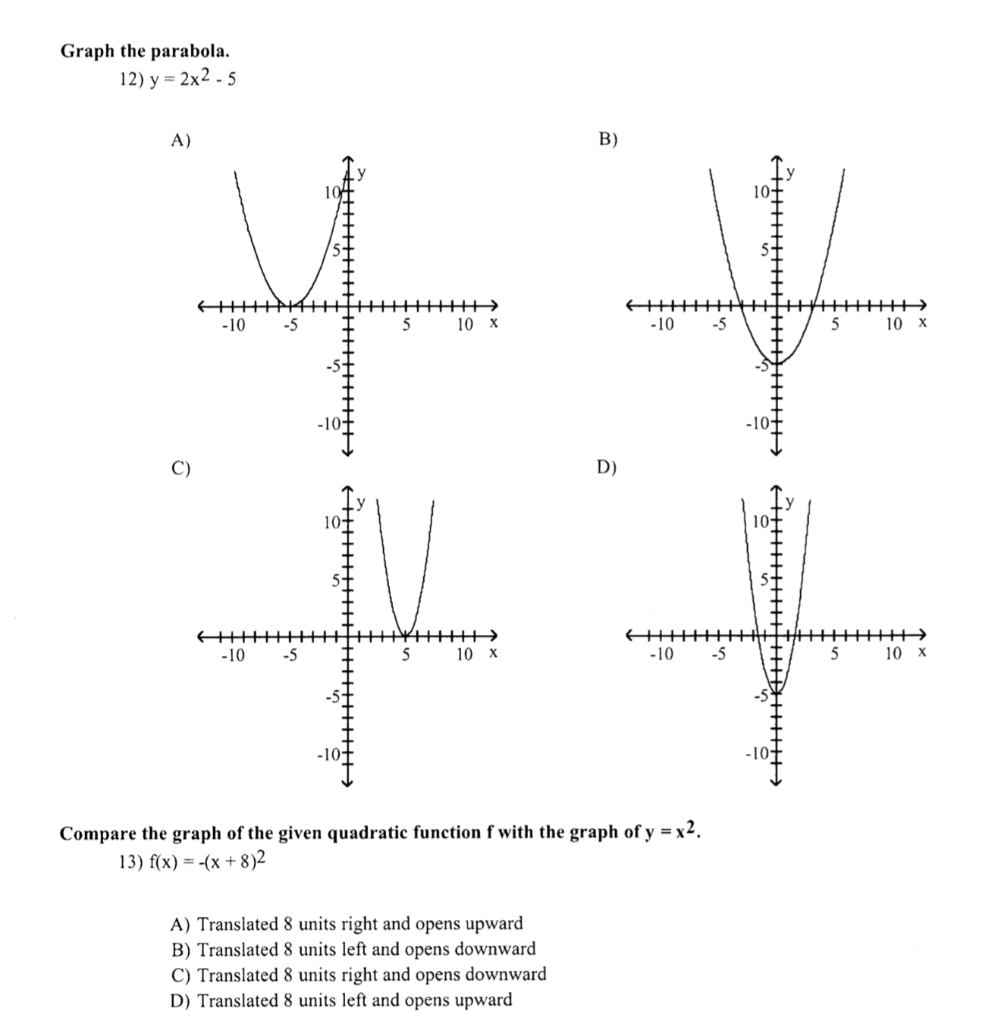



Solved Graph The Parabola 12 Y 2x2 5 A B 10 Chegg Com




The Aim Of This Powerpoint Is To Enable You To Quickly And Easily Draw The Graphs Of Parabolas When Given Their Equations It Will Show You How To Determine Ppt Download



Graphing And Properties Of Parabolas Kuta Software




How To Graph A Parabola 13 Steps With Pictures Wikihow
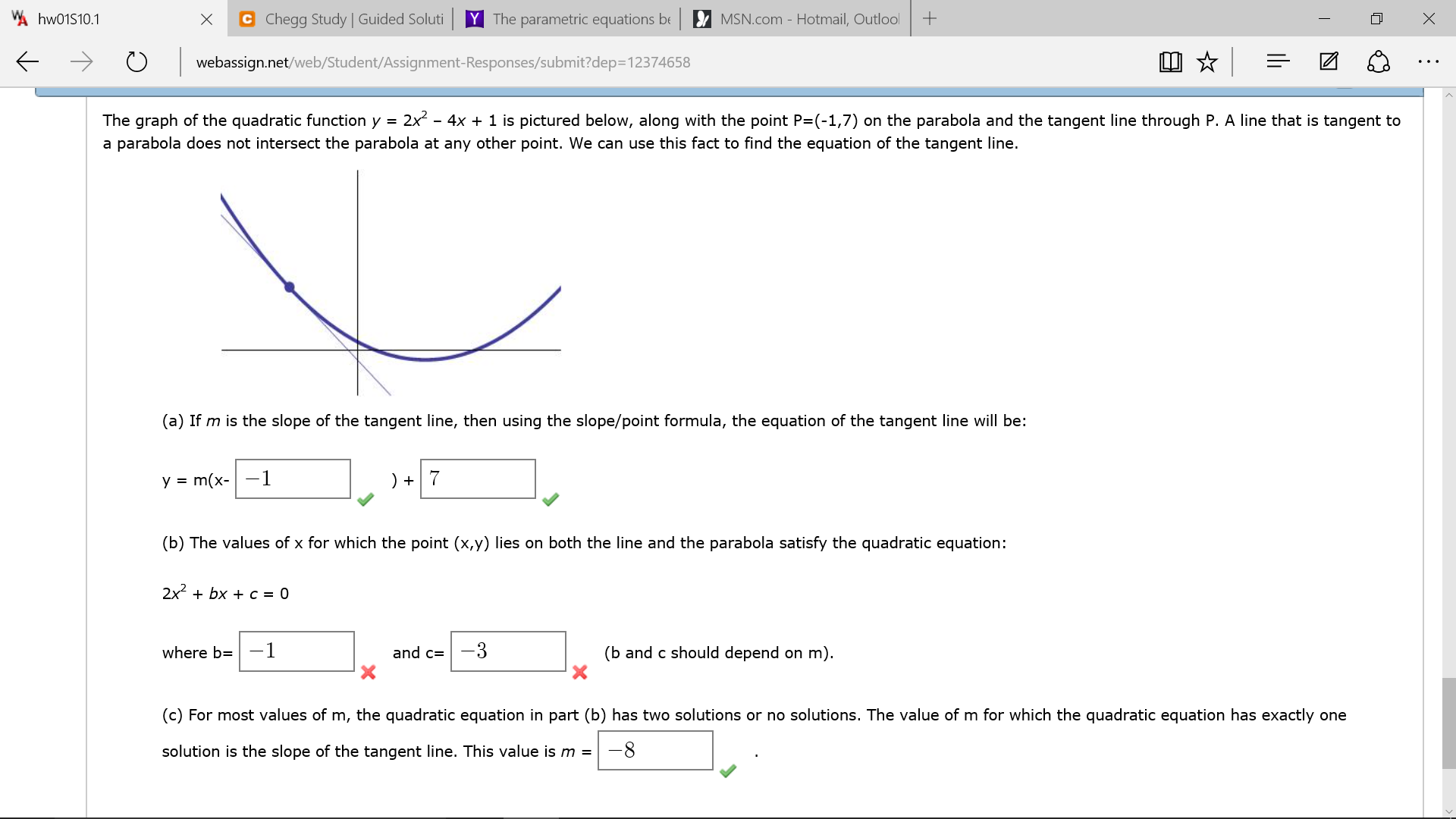



Solved The Graph Of The Quadratic Function Y 2x 2 4x 1 Chegg Com
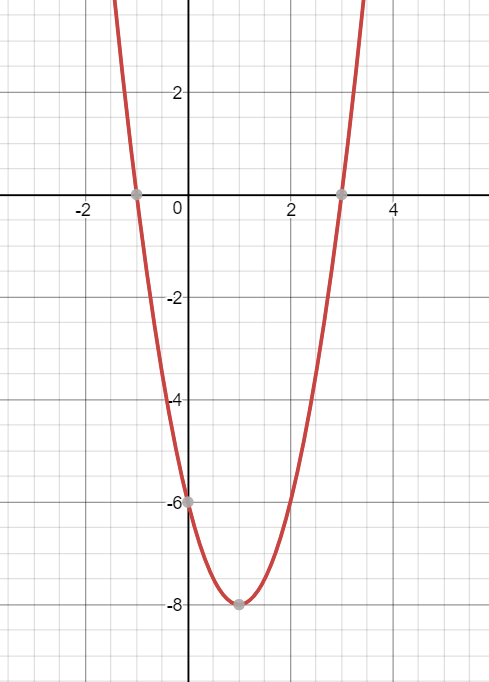



What Is The Axis Of Symmetry And Vertex For The Graph Y 2x 2 4x 6 Socratic



Solution Graph The Quadratic Equation Y 2x 2 What Is The Vertex Also Graph The Parabola If You Can Please Include The Points That I Have To Graph Plot That Would Be G



How Will You Find The Area Of The Region Bounded By The Parabola Y Squared Is Equal To 4 X And The Line Y Is Equal To 2x Quora
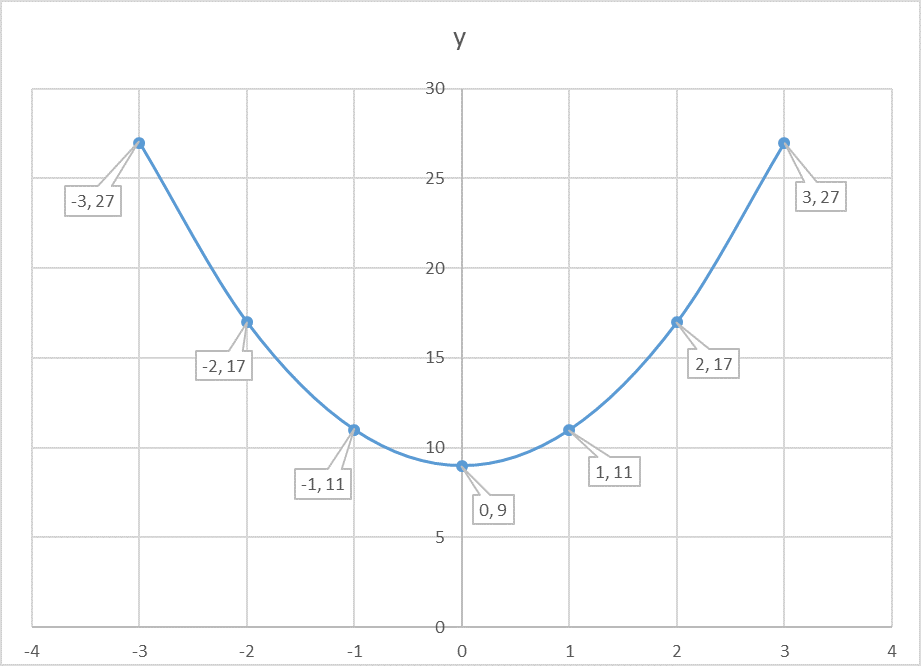



How Do You Graph The Parabola Y 2x 2 9 Socratic



Graphs Of Functions Y X2 Y 2x2 And Y 2x2 In Purple Red And Blue Respectively



Stephani Eckelkamp The Parabola Friend Of Foe The Graph Of A Parabola Y X2 Has A Vertex At 0 0 The Graph Is Shown Below Now Let Us Look At The Graph Y Ax2 Where A 1 2 3 10 1 3 And 1 10 And When A 1 2 3 10 1 2 1 3 And 1 10




Quadratic Graph Example Y Ax Expii



Solved Determine The Zeros Of Y 2x 2 12x 5 Course Hero




6 The Graph Of The Parabola Given By The Function Y 2x2 2x 1 Opens Up Or Down Incorrect Your Answer Down Correct Answer Down Explanation The 2 In Y 2x2 2x 1
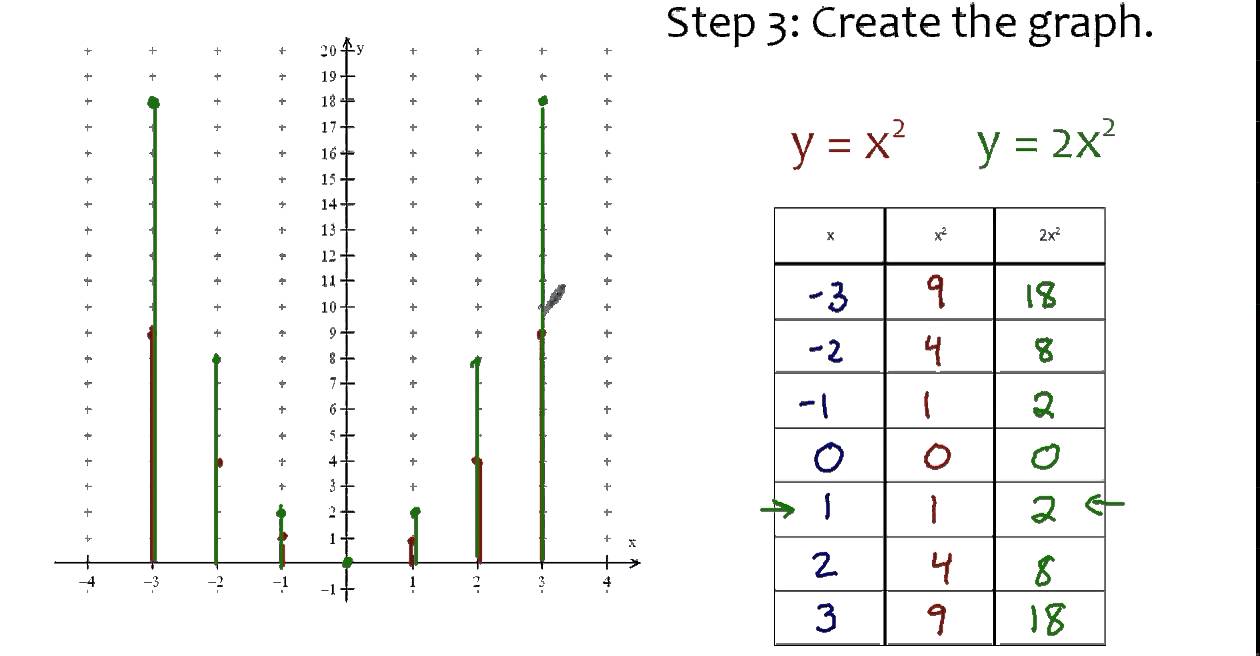



Y 2x 2 Youtube



Y 2x 1




How To Draw Y 2 X 2 Interactive Mathematics




Is The Parabola Described By Y 2x 2 Wider Or Narrower Than The Parabola Described By Y X 2 Socratic




Find The Point On The Curve Y 2x 2 6x 4 At Which The Tangent Is Parallel To The X Axis Youtube




Use The Parabola Tool To Graph The Quadratic Function Y 2x2 12x 14 Graph The Parabola By First Brainly Com



Mathscene Functions 1 Lesson 3
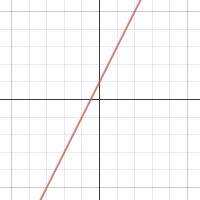



Y 2x 1



For The Equation Y 2x 2 How Do I Find The Focus And The Directrix Of That Parabola Explaining All The Steps Quora




How Do You Graph The Parabola Y 2x 2 4 Using The Vertex Intercepts And Additional Points Study Com




Content Transformations Of The Parabola



Sketching Quadratics



Draw The Graph Of Y 2x 2 X 6 Mathskey Com



Y 2x 2 Graph
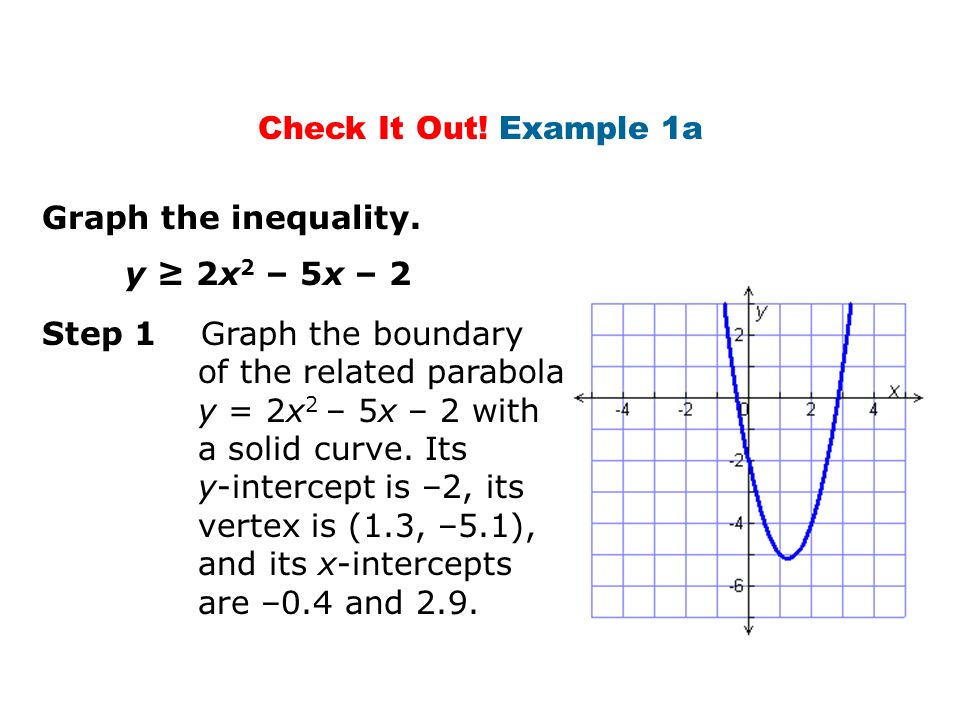



Warm Up 1 Graph The Inequality Y 2x 1 Solve Using Any Method 2 X 2 16x 63 X 2 8x 3 7 Ppt Download
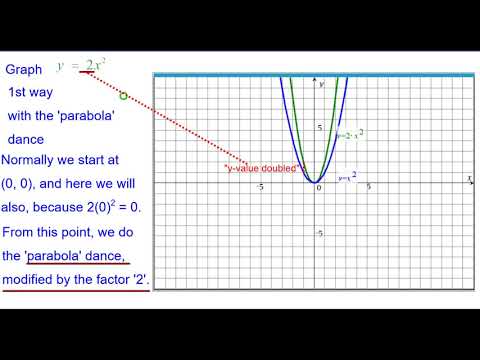



01da Quick Graph Y 2x 2 Youtube




The Focus Of The Parabola Y 2x 2 X Is A 0 0 B 1 2 1 4 C 1 4 0 D Youtube



Untitled Document



0 件のコメント:
コメントを投稿